Отзывы о казино 1Win от реальных игроков

После проведения анализа оставленных игроками отзывов о казино 1Win, мы можем сделать выводы о качестве предоставляемых услуг. Многие игроки высоко оценили сайт казино и отметили его простоту и удобство использования.
Однако, по отзывам, также были замечены некоторые проблемы в работе сервиса, связанные с неполадками интерфейса и производительностью сайта. Несмотря на это, игроки положительно отозвались об игровом ассортименте и бонусной программе казино 1Win.
Игроки также отметили, что казино 1Win выполняет свои обязательства по выплатам выигрышей в полном объеме и в срок. Кроме того, система финансовых операций на сайте казино довольно удобна и понятна в использовании.
|
🔥 Официальный сайт |
28july.ru |
|
🎰 Год основания |
2023 |
|
📄 Лицензия |
Предоставлено и действует в соответствии с законодательством Кюрасао, как согласовано с Antillephone N.V. в лицензии на игру. Номер игровой лицензии — 8048/JAZ 2019-055. |
|
🙌 Владелец |
NestlingCorn Limited |
|
🎲 Игр |
3000+ |
|
🗺️ Языки |
русский, украинский, английский, немецкий, испанский, итальянский, арабский, румынский, португальский, шведский, польский, норвежский, финский, болгарский, японский, китайский, турецкий, азербайджанский, французский, литовский, чешский, греческий, хорватский, сербский, вьетнамский, узбекский, грузинский, тайский, корейский, латышский, казахский, индонезийский, словенский, персидский, иврит, хинди, малайский, албанский, белорусский, армянский, датский |
|
💵 Валюты |
USD, EUR, RUB, UAH, CAD, AUD, JPY, KZT, MDL, BYN, BTC, AED, ALL, AMD, AOA, AZN, BAM, BDT, BGN, BHD, BIF, BOB, BRL, BWP, CDF, CHF, CLP, GHS, GMD, GNF, HKD, HRK, HTG, JOD, KES, KGS, KRW, KWD, MGA, MKD, MMK, NAD, NGN, NOK, NPR, NZD, RON, RSD, RWF, SAR, SCR, SDG, SOS, SZL, THB, TJS, TMT, TND, TRY, TWD |
|
🧑💻 Провайдеры |
Microgaming, Quickspin, Evolution Gaming, ELK Studios, Playson, Red Tiger, Push Gaming, iSoftBet, Pragmatic Play, Habanero, Genesis Gaming, 1x2 Gaming, Kalamba Games, Rabcat, Foxium, Big Time Gaming, Booming Games, Thunderkick, EGT, Amatic, Betsoft, Endorphina, GameArt, PariPlay, Bgaming, Igrosoft, Rival, Red Rake, Ezugi, Booongo, Genii, Iron Dog Studio, Tom Horn Gaming, Authentic Gaming, Spinomenal, Blueprint Gaming, Realistic Games, Wazdan, Belatra, Evoplay, Platipus, Vivo Gaming, Lucky Streak, Felix Gaming, Swintt, Oryx, August, Leap Gaming, Fantasma Games, Gamefish Global, JFTW, Apollo Games, Mr.Slotty, BF Games, Gamomat, Pg Soft, Fugaso, Multislot, Spigo, Worldmatch, Netgame, Ruby Play, Sa Gaming, Reelnrg, Bbin, Betixon, Evolution Slots, Espresso Games, N2-Live, Noble, Portomaso Gaming, Radi8, VRCasino, Gamzix, Live Solutions, Up Games |
|
💳 Методы депозита |
VISA, MasterCard, WebMoney, UzPay, PayTM Wallet, UPI, AirTM, HOTVouchers, GrataPay Vouchers, PayGiga, Paytrust88, Hizli, Santander, Multibanco, Caixa, Bradesco, Banco de Brazil, Itau, Pay4Fun, Papara, FastPay, Vcreditos, Flexepin, Trues USD, Nemo, Amigo, B-pay, BitShares, Ethereum Classic, Basic Attention Token, OmiseGO, Chainlink, Paxos Standard Token, USD Coin, Tron, Stratis, QTUM, Verge, Bitcoin Gold, DigiByte, Monero, Sticpay, Epay, TelePay, Zcash, Jeton Wallet, Piastrix, Dash, Tether, Dogecoin, Boleto Bancario, Bitcoin Cash, MuchBetter, Litecoin, Ripple, Ethereum, ecoPayz, МИР, Astropay |
|
💳 Методы вывода |
Astropay, VISA, MasterCard, МИР, ecoPayz, Bitcoin, Ethereum, Ripple, Litecoin, Maestro, Bitcoin Cash, Payeer, Dogecoin, Tether, Dash, NEM, Piastrix, Jeton Wallet, Zcash, Sticpay, Monero, DigiByte, Bitcoin Gold, Verge, QTUM, Stratis, Tron, USD Coin, Paxos Standard Token, Chainlink, OmiseGO, Basic Attention Token, Ethereum Classic, BitShares, B-pay, Trues USD, Sepa |
|
🎁 Бонус |
100% на первый депозит, 100% релоад + 5 вращений на Колесе Фортуны, 5% кэшбэк |
|
💰 Мин. депозит |
100 руб. |
|
💸 Мин. вывод |
100 руб. |
|
📱 Мобильная версия |
Android, iOS, Windows |
|
💬 Служба поддержки |
|
Безопасность и лицензирование казино 1Win также вызвали доверие у игроков, что становится еще одним плюсом данного игрового ресурса.
Обзор казино 1Win
1Win – это казино с более чем 10 летней историей работы. За это время онлайн-площадка сумела завоевать доверие множества игроков со всего мира. Казино полностью лицензировано, что гарантирует безопасность и честность игры.
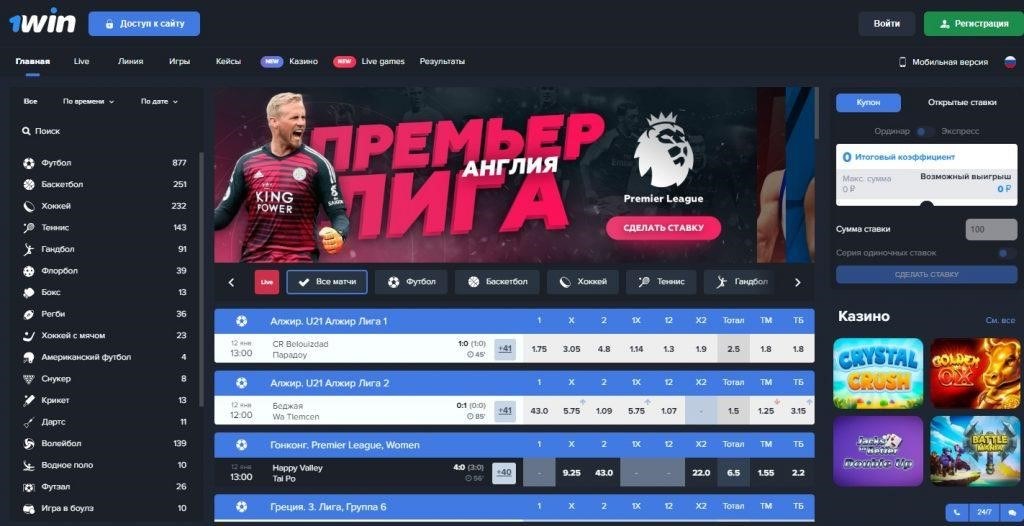
Официальный сайт казино имеет яркий и привлекательный дизайн. На главной странице размещены актуальные бонусные предложения, новости, а также разнообразная информация об играх и сервисах.

Казино предлагает широкий выбор различных игровых автоматов, столовых игр, а также игр в режиме реального времени с живыми дилерами. Все игры доступны в браузере, без необходимости скачивать дополнительное программное обеспечение.
| Преимущества: | Недостатки: |
|---|---|
|
|
В целом казино 1Win является надежным и уважаемым игровым порталом, который предлагает широкий выбор игр и привлекательные бонусные предложения. Система защиты гарантирует безопасность пользователей, а квалифицированные работники технической поддержки всегда готовы помочь и ответить на интересующие вопросы.
Регистрация на сайте
Чтобы начать играть в казино 1Win, необходимо зарегистрироваться на сайте. Регистрация здесь проходит быстро и просто.
Для этого нужно нажать на кнопку "Регистрация", которая находится в верхней части сайта и заполнить все необходимые данные в специальной форме. Это обычный процесс, который вы уже могли видеть на других сайтах.
Перед регистрацией убедитесь, что вы ознакомились с правилами и условиями казино. Важно, чтобы ваши данные были введены правильно, чтобы последующие финансовые операции были выполнены без проблем.

Игровой ассортимент
Казино 1Win предлагает своим игрокам огромный выбор игровых автоматов от лучших разработчиков, таких как NetEnt, Microgaming, Quickspin, Play'n GO и другие. Разнообразие слотов включает в себя классические игровые автоматы, видео слоты с различными тематиками, игры с прогрессивным джекпотом и многое другое.
Помимо слотов, на сайте вы найдете карточные игры, рулетку, видеопокер, а также возможность сделать ставки на спортивные события. Кроме того, в казино регулярно проводятся турниры и лотереи с призами, что делает игровой процесс еще более увлекательным и интересным.
Безопасность и лицензирование
Казино 1Win работает на основе лицензии, выданной Кюрасао. Это означает, что казино проходило строгие проверки и удовлетворяет необходимым стандартам безопасности и честности. Все игры казино 1Win проверены независимыми аудиторами на справедливость и случайность и имеют соответствующие сертификаты.
Кроме того, казино использует современные технологии защиты информации, так что все данные игроков, в том числе финансовые, хранятся в безопасности и не могут быть использованы третьими лицами.
Финансовые операции
Казино 1Win предлагает своим игрокам удобную и безопасную возможность реализовать все финансовые операции. Для этого на сайте доступны самые распространенные платежные системы:

- Visa
- MasterCard
- Яндекс.Деньги
- WebMoney
- QIWI
- И другие
В казино 1Win вы можете сделать депозит от 300 рублей. Дополнительных комиссий за внесение денег не будет.
Что касается вывода средств, то все заявки обрабатываются оперативно. Средства можно вывести на ту же платежную систему, которая использовалась для депозита. Если у игрока есть вопросы, то можно обратиться в службу поддержки, которая работает круглосуточно.
| Платежная система | Мин. сумма ввода | Срок зачисления на счет | Комиссия |
|---|---|---|---|
| Visa | 300 рублей | Мгновенно | 0% |
| MasterCard | 300 рублей | Мгновенно | 0% |
| Яндекс.Деньги | 300 рублей | Мгновенно | 0% |
| WebMoney | 300 рублей | Мгновенно | 0% |
| QIWI | 300 рублей | Мгновенно | 0% |
Стоит отметить, что при выводе средств может потребоваться подтверждение личности игрока. Это связано с необходимостью предотвращения мошенничества и защитой финансовых операций.
Отзывы игроков о казино 1Win
Игроки, выбравшие казино 1Win, оставляют как положительные, так и отрицательные отзывы об этой платформе. Среди самых популярных тем, которые затрагивают игроки, можно выделить выигрыши и выплаты, бонусную программу и общее впечатление от игры.
Многие игроки отмечают высокий процент выплат на сайте 1Win, а также быстрые и безопасные транзакции. Некоторые даже делятся своим счастьем, рассказывая о нескольких крупных выигрышах на этой платформе.
Однако есть и те, кто сталкивался с проблемами при вводе/выводе денег, а также с техническими неполадками в работе сайта. Они высказывают свои недовольства и желание улучшить качество обслуживания.
Бонусная программа казино 1Win также вызывает разные реакции у игроков. Кто-то отмечает ее щедрость и удобство использования, а кто-то настаивает на ее несоответствии со заявленными условиями.
Несмотря на разную точку зрения у игроков, общее впечатление от казино 1Win все же вполне положительное. Платформа предлагает разнообразный ассортимент игровых автоматов и настольных игр, ориентированный на различных пользователей.
Выигрыши и выплаты
Казино 1Win предлагает игрокам большой выбор игровых автоматов с высокими шансами выигрыша. Многие игроки высказываются положительно о выигрышах, которые они получают в этом казино. Однако, как и в любом другом казино, есть ситуации, когда игроки проигрывают деньги.
По отзывам игроков, казино 1Win оперативно выплачивает выигрыши. Средний срок ожидания проверки заявки на вывод денег составляет от 24 до 48 часов. Затем деньги поступают на счет игрока в течение нескольких банковских дней.
Однако, стоит учитывать, что на сроки выплат может повлиять выбранный игроком метод вывода денег. Рекомендуется обращаться к службе поддержки казино, чтобы уточнить детали процесса выплат и выбрать наиболее быстрый и удобный способ.
Бонусная программа
Казино 1Win предлагает разнообразные бонусы и акции для своих игроков. Новичкам доступен приветственный бонус в размере до 500 долларов, а также бесплатные спины в слотах. Для постоянных игроков периодически проводятся турниры и лотереи с щедрыми призами.
Одним из главных преимуществ программы лояльности является кэшбэк. В зависимости от уровня игрока, ставок и проигрышей, на счет возвращается определенный процент денежных средств. Кроме того, можно заработать баллы за активность и обменять их на реальные деньги или фриспины.
Важно отметить, что все бонусы и акции связаны с определенными условиями. Обязательно ознакомьтесь с правилами проведения акций на сайте казино.
| Критерии | Плюсы | Минусы |
|---|---|---|
| Регистрация на сайте | Процесс регистрации простой и быстрый | Отсутствие возможности регистрации через социальные сети |
| Игровой ассортимент | Большой выбор игр от лучших провайдеров | Ограниченный выбор игр в живом казино |
| Безопасность и лицензирование | Казино имеет лицензию, обеспечивает безопасность пользователей | Нет двухфакторной аутентификации |
| Финансовые операции | Казино предлагает различные способы внесения и вывода денег | Некоторые методы занимают достаточно много времени на обработку операций |
| Выигрыши и выплаты | Казино быстро и честно выплачивает выигрыши | Некоторые пользователи жалуются на задержки при выводе денег |
| Бонусная программа | Казино предлагает множество бонусов и акций для игроков | Вейджер на бонусы может быть достаточно высоким |
| Общее впечатление игроков | Многие игроки довольны казино и рекомендуют его | Некоторые жалобы на поддержку и на некоторые технические проблемы при игре |
Общее впечатление игроков
1. Оценка игрового процесса:
- Большинство игроков отмечают, что игровой процесс в казино 1Win очень увлекательный, интересный и наполненный множеством разнообразных возможностей.
- Многие отмечают, что выбор игр очень впечатляющий и разнообразный, что позволяет подобрать оптимальный вариант для каждого пользователя.
- Оценки за атмосферу, графику и звук в игровых автоматах также очень высокие.
2. Уровень сервиса и техническая поддержка:
- Игроки отмечают, что сервис в казино 1Win на очень высоком уровне. Все вопросы решаются быстро и качественно.
- Техническая поддержка работает круглосуточно и готова помочь в любой момент. Пользователи оставляют отзывы, что они всегда получают квалифицированную помощь в любой ситуации.
3. Выплаты и финансовые операции:
Часто задаваемые вопросы
Какой минимальный депозит можно сделать на казино 1Win?
Минимальный депозит на казино 1Win составляет 100 рублей. Однако, для получения бонуса на первый депозит сумма должна быть не менее 500 рублей.
Какие игры доступны в казино 1Win?
В казино 1Win доступно более 2000 слотов от ведущих провайдеров, также есть возможность сыграть в многоканальную рулетку, блэкджек, баккару и другие настольные игры.
Как долго обрабатываются запросы на выплаты выигрышей?
Обработка запросов на выплаты выигрышей на казино 1Win занимает от 10 минут до 24 часов в зависимости от выбранного способа выплаты.
Какие методы оплаты принимает казино 1Win?
Казино 1Win принимает оплату банковскими картами, электронными кошельками, мобильным телефоном, а также криптовалютой.
Какие бонусы предоставляет казино 1Win?
Казино 1Win предоставляет бонус на первый депозит, фри-спины в различных играх, кэшбэк и многие другие акции. Информацию о бонусах можно найти на сайте казино.
Как защищены данные пользователей на казино 1Win?
Данные пользователей на казино 1Win защищены с помощью современных технологий шифрования, а также хранятся на защищенных серверах, к которым доступ имеют только авторизованные сотрудники казино.
Обновлено: 2023-05-19
- Возможность вывода выигрышей является одним из наиболее важных параметров для большинства игроков. В казино 1Win выигрыши выплачиваются вовремя, что подтверждают отзывы реальных пользователей.
- Игроки также отмечают удобство проведения финансовых операций. Система ввода и вывода денег очень проста и интуитивно понятна. В сервисе доступны различные платежные системы, что позволяет выбрать наиболее удобный способ для каждого пользователя.